Chapter 6. Relative and Absolute Dating
Overview of Relative and Absolute Dating
Adapted by Sean W. Lacey & Joyce M. McBeth (2018) University of Saskatchewan from Deline B, Harris R, & Tefend K. (2015) “Laboratory Manual for Introductory Geology”. First Edition. Chapter 1 “Relative and Absolute Dating” by Bradley Deline, CC BY-SA 4.0. View Source.
6.2 Geologic Time
The methods that geologists use to establish relative time scales are based on geologic laws and principles. A scientific law is something that we understand and is proven, and a principle is a guide we use to help us evaluate a system. Geologic laws and principles are generally easy to understand and simple. Geologists use stratigraphic principles – rules that help us interpret relationships between rocks – to describe and interpret relationships between layers and types of rock and determine the relative ages of rocks and geologic events (i.e., the order in which they formed or occurred).
To provide context for the stratigraphic principles, we’ll begin this section with a review of the different rock types. Sedimentary rocks (e.g., sandstone) are made from broken pieces of other rock that are eroded in the high areas of the earth and transported by wind, ice, and water to lower areas where they are deposited. Igneous rocks form through cooling and crystallizing of molten rock. Metamorphic rocks form when heat and pressure cause recrystallization within rocks, which can alter the mineralogy and/or texture. This distinction is important because these three rock types are formed differently and therefore, the events that lead to their formation are interpreted differently when assessing the rock record using geologic laws and principles.
To interpret stratigraphic relationships between geological units (types and layers of rock), geologists use geologic cross-section diagrams (e.g., Figure 6.1). These are drawings that illustrate the relationships between rocks if you cut into the earth and look at the layers of rock below the surface. A useful analogy for a cross-section is a piece of layered cake: if you cut a piece of the cake and remove it, viewed from the side you will see the top layer of icing, the cake layer beneath it, and then layers of filling and cake alternating as you go deeper into the cake (moving down the slice from the surface at the top of the cake). Geologists use data including maps based on rock outcrops at the surface, cores drilled from the rock, and geophysical data (e.g., seismic data) to help construct cross-sections.
There are 7 stratigraphic principles that geologists use to relatively date rock units:
- law of superposition
- principle of original horizontality
- principle of lateral continuity
- principle of cross-cutting relationships
- principle of unconformities
- principle of inclusions
- principle of faunal succession
The law of superposition states that in an undeformed sequence of sedimentary rocks the oldest rocks will be at the bottom of the sequence while the youngest will be on top. Imagine a river carrying sand into an ocean, the sand will spill out and come to rest on top of the seafloor. This sand was deposited after the sand of the seafloor was already deposited, so it is deposited above the seafloor sediments. Over time, more layers can be deposited on top of the sand as sediments are carried into the ocean by rivers and deposited. We can then create a relative time scale of rock layers from the oldest rocks at the bottom (labeled#1 in Figure 6.1) to the youngest at the top of an outcrop (labeled #7 in Figure 6.1).

Source: Bradley Deline (2015) CC BY-SA 3.0 view source
The principle of original horizontality states that undeformed sedimentary rock are deposited horizontally. The deposition of sediment is controlled by gravity and will pull it downward. If you have muddy water on a slope, the water will flow down the slope and pool flat at the base rather than depositing on the slope itself. This means that if we see sedimentary rock that is tilted or folded it was first deposited flat, then folded or tilted afterward (Figure 6.2).
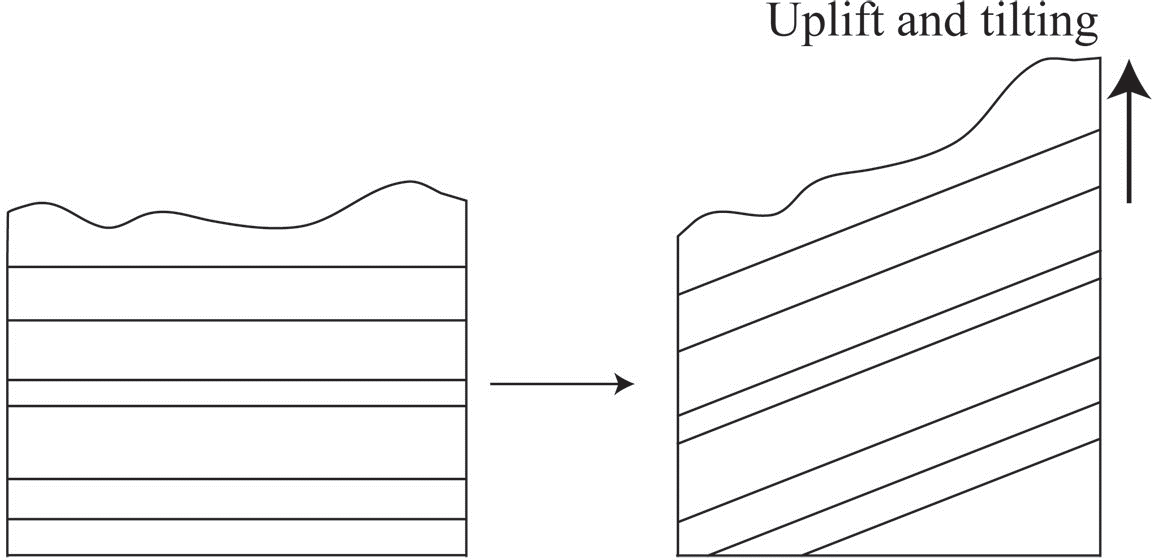
Source: Bradley Deline (2015) CC BY-SA 3.0 view source
Sedimentary rock are generally deposited continuously in all directions. Sometimes erosion can lead to lateral gaps forming in layers of the rock. For example, when a stream erodes through a rock layer. The principle of lateral continuity states that even though the rocks are separated from one another by a gap, they were originally part of the same unit (layer) of rock.
The principle of cross-cutting relationships states that when two geologic features intersect, the one that cuts across the other is younger. In essence, a feature has to be present before something can affect it. For example, if a fault fractures through a series of sedimentary rocks those sedimentary rocks must be older than the fault (Figure 6.3).

Source: Bradley Deline (2015) CC BY-SA 3.0 view source
In geology, rocks that are missing are sometimes as important as rocks that still exist in the rock record; what is missing is very important for building a complete geologic history! Unconformities are surfaces that represent significant weathering and erosion (the breakdown of rock and movement of sediment) which result in missing or erased time in the rock record. Erosion often occurs in elevated areas like continents or mountains. Uplift, which often occurs when rocks are pushed up by tectonic activity, results in erosion. This will destroy a part of the rock record sequence. Much older rocks are then exposed at the earth’s surface, with a gap where the younger rocks were previously. If the area sinks (called subsidence), then much younger rocks will be deposited on top of these exposed rocks. The amount of time missing can be relatively short or may represent billions of years.
There are three types of unconformities based on the types of rocks present above and below the unconformity (Figure 6.4). A nonconformity is an unconformity where the rock type is different above and below the unconformity (Figure 6.4). For example, if uplifted intrusive igneous rocks are exposed at the surface and then covered with sedimentary rock, the boundary between the two rock types is a nonconformity. If the rocks above and below the erosion surface are both sedimentary, then the orientation of the layers is important. If the rocks below the erosion surface are not parallel with those above, the surface is called an angular unconformity (Figure 6.4). This is often the result of the rocks below being tilted or folded prior to the erosion and deposition of the younger rocks. If the rocks above and below the erosion surface are parallel, the surface is called a disconformity. This type of surface is often difficult to detect, but can often be recognized using other information such as the fossils discussed in the next section. Paraconformity is a term used to describe a disconformity where the unconformity surface is very difficult to detect and can only be detected using absolute dating techniques (e.g., radiometric dating of zircons).
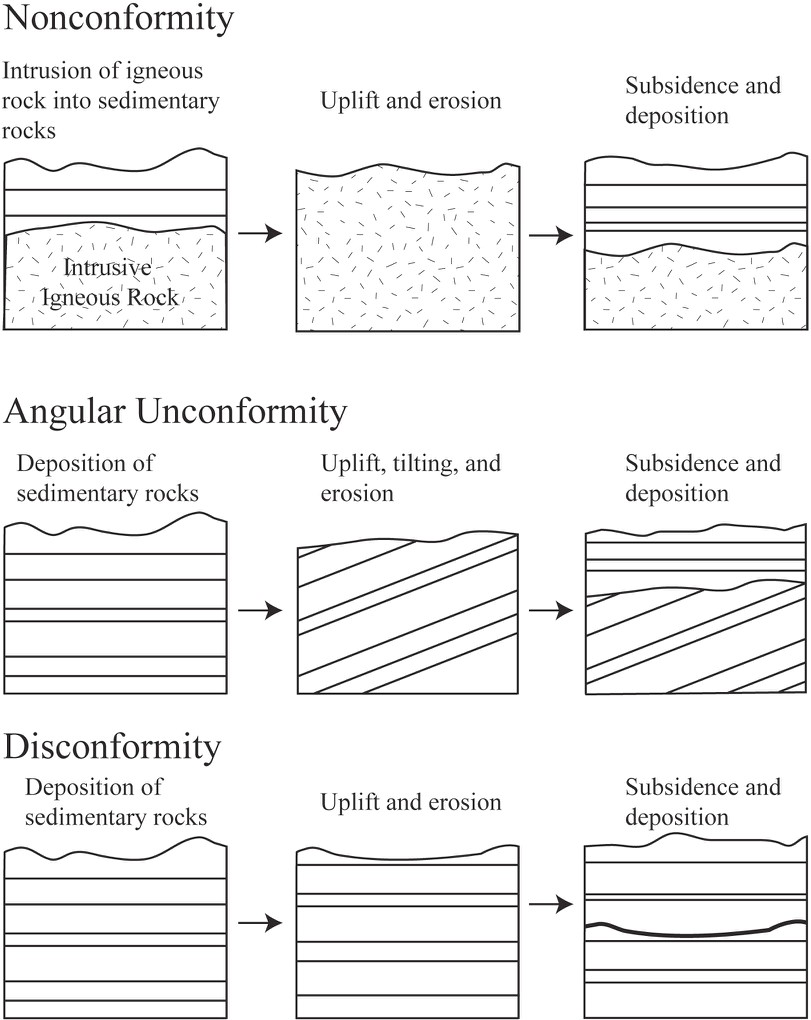
Source: Bradley Deline (2015) CC BY-SA 3.0 view source
There are two other stratigraphic principles to be aware of, though we won’t practice applying these two principles in the lab exercises for this chapter. The principle of inclusions states that if inclusions (pieces of rock) are found within a rock formation, those inclusions must be older than the formation they are included within. For example, conglomerates are sedimentary rocks with gravel or cobble sized stones cemented together; the stones within the conglomerate are composed of rock that are older than the conglomerate. The principle of faunal succession is a stratigraphic principle where geologists use fossils in the rock to help interpret the relative ages of the rock.
We can use these principles to determine the relative ages of a series of rocks in a geologic cross-section. We can also use this information to create a hypothesis about the series of geologic events that created and affected the rocks in the cross-section through time. Common events that are often preserved as evidence in the rock record include: (1) deposition of sedimentary layers, (2) tilting or folding of rocks, (3) uplift and erosion of rocks, (4) intrusion of magma that solidifies into intrusive igneous rocks, and (5) fracturing of rock (faulting). Figures 6.5 and 6.6 show how to piece together a series of geologic events using relative dating.
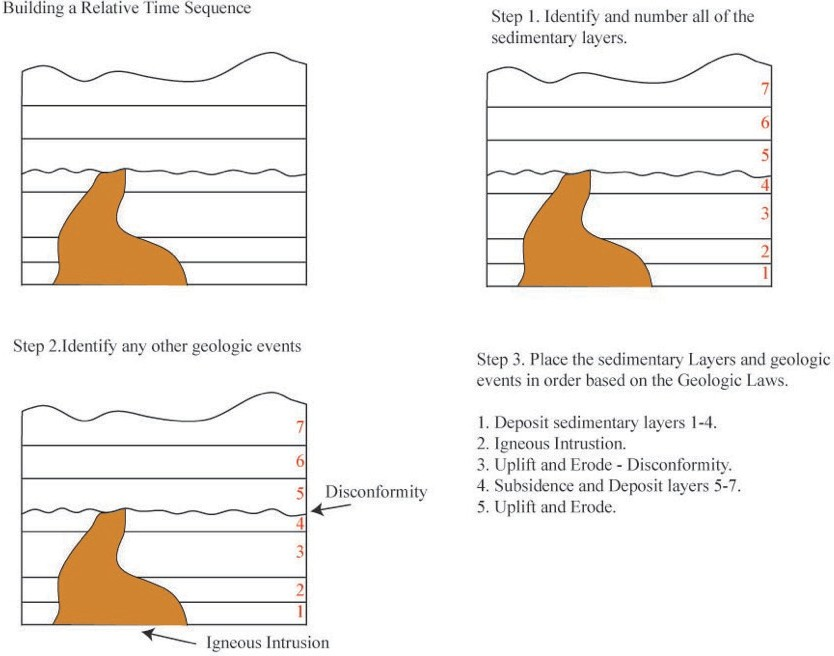
Source: Bradley Deline (2015) CC BY-SA 3.0 view source
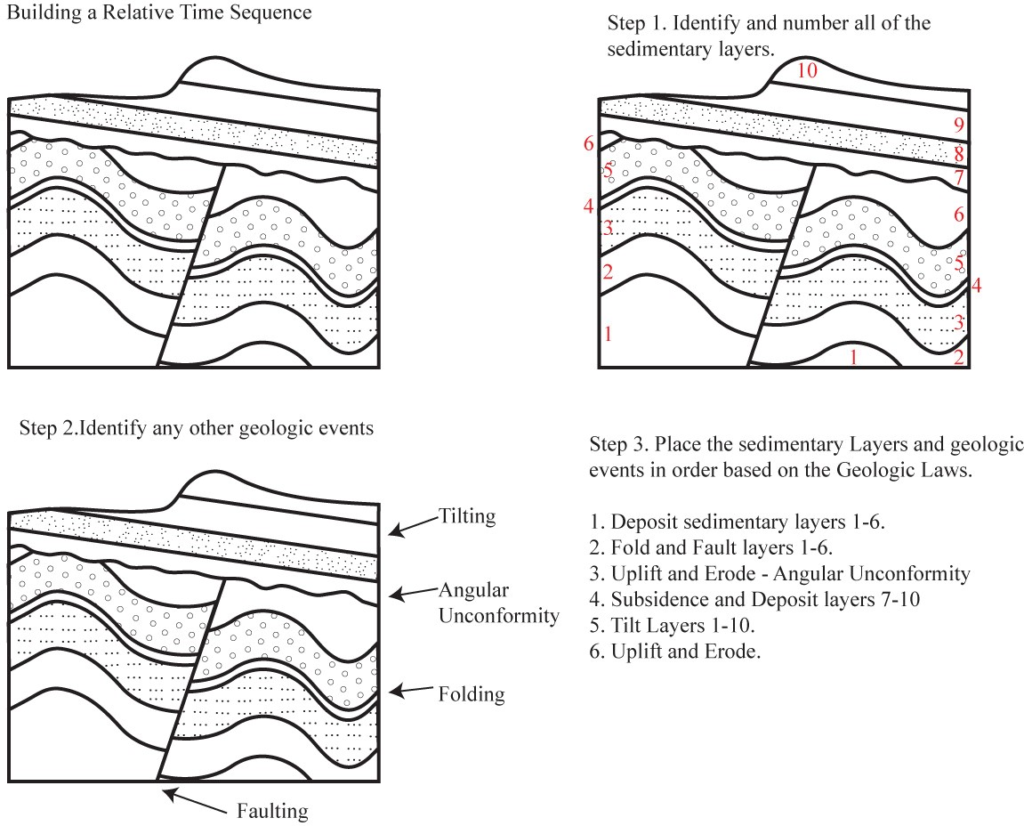
Source: Bradley Deline (2015) CC BY-SA 3.0 view source
6.3 ABSOLUTE AGE AND RADIOMETRIC DATING
Absolute age of a rock or object is different from relative age. With absolute age dating, scientists determine the absolute age of a rock in millions of years before present rather than just the age of the rock relative to the rock units around it. This information helps geologists develop more precise geological history models for the rocks and regions they study. Absolute age is generally determined using a technique called radiometric dating, which uses radioactive isotopes of elements in the rock to estimate the age of the rock.
Atoms are made of three particles: protons, electrons, and neutrons. All three of these particles are important to the study of geology: the number of protons defines the identity of a particular element (e.g., carbon has 6 protons), the number of electrons control how that element bonds to other elements to make compounds, and the number of neutrons changes the atomic weight of an element. Isotopes are atoms of an element that differ in the number of neutrons in their nucleus and, therefore, their atomic weight.
Some isotopes are unstable and decay (break down into other isotopes) over time. This process is called radioactive decay. In radioactive decay, a particle (e.g., a neutron, electron, or x-ray photon) is emitted from a radioactive atom, called the parent atom. After the particle is emitted the parent atom is altered to form a different isotope (often a different element) called the daughter atom. To be useful for radiometric dating, the daughter isotope atom should not be radioactive (i.e., it should not disappear once it has formed).
Scientists have studied and measure the radioactivity of different elements in the lab to calculate the rate of decay for each isotope. Though the rate of decay varies between isotopes from milliseconds to billions of years, each isotope decays at a regular and predictable rate. This is called the half-life of the isotope. The half-life is defined as the amount of time it takes for half of the atoms of the radioactive parent isotope to decay to atoms of the daughter isotope. The half-life is independent of the amount of atoms at a given time; for example, it takes the same amount of time for the amount of parent isotope to decrease from 100% to 50% as it takes for the amount of the parent isotope to decrease from 50% to 25% of its original value. If we plot this pattern as a plot of time vs atoms remaining, we get a radioactive decay curve. When a rock initially forms there are generally very few daughter atoms present in the rock; thus, if we know the length of the half-life for a particular radioactive isotope and we measure the amount of parent and daughter isotope in a rock, we can then calculate the age of the rock. This is the basis for radiometric dating. The concentrations of the different isotopes are measured using an instrument called an isotope ratio mass spectrometer. Given the shape of the radioactive decay curve, a material theoretically never completely runs out of the parent isotope. In practice, scientists can only effectively measure the concentration of remaining parent isotope up to 10-15 elapsed half-lives; after that the concentration of parent isotope remaining is generally too low in concentration to measure.
6.4 RADIOMETRIC DATING SYSTEMS
There are several different pairs of radioactive isotope parent and daughter atoms that are commonly used to absolutely date rocks. Each of these radiometric dating systems (or isotopic dating methods) has different uses within geology; due to the differences in the half-lives and chemistry of the isotopes they are useful for dating objects over certain age ranges or composed of certain materials.
For example, radiocarbon (Carbon-14) dating is of limited use within geology because of the relatively short half-life of Carbon-14 in comparison with the scale of geologic time. However, more people have heard of this radiometric dating system than the others used in geology, because radiocarbon dating is used extensively in archaeology. Carbon-14 (the parent isotope) is found in organic material including bone, tissue, plants, and fiber. This isotope is found naturally in small amounts in the atmosphere within CO2 and is incorporated into plants when they grow. The plants are consumed by animals, which are consumed by other animals and so on, and thus the carbon-14 thus moves throughout the food chain. You currently have carbon-14 in your body that is decaying to nitrogen-14 (the daughter isotope). As we eat, we replace any carbon-14 we excrete. When an animal stops eating or a plant stops growing (e.g., when a tree is cut down to use for building a home), the radioactive carbon starts to decay without being replaced. This change in carbon-14 concentration can be measured using radiometric dating techniques to determine how long it has been since the animal or plant died (and in the case of a house, this will probably coincide with when it was built). Carbon-14 has a very short half-life of 5,730 years and can thus only be used to date materials up to approximately 70,000 years old. Over that age, there would not be enough parent isotope atoms left to get accurate dating information using this isotopic dating method. Given the age of the Earth is 4.54 billion years, carbon-14 can only be used to date very recent materials.
Uranium-lead (U-Pb) dating – also known as U-Pb geochronology – involves decay of the isotope Uranium-238 through many different daughter isotopes that are also radioactive until the atom reaches the non-radioactive lead-206 isotope. Surprising to most students, uranium can be found in many places, but it is normally present in miniscule amounts so does not pose a radioactive hazard. One challenge with this system is that the daughter isotope lead-206 is also found naturally in many different places; this makes it difficult to differentiate between lead formed from radioactive decay and lead found naturally in the environment. The mineral zircon solves both of these issues, by concentrating uranium and excluding lead from its mineral structure. Therefore, we use uranium dating on zircons found within igneous rocks (such as volcanic ash or rocks formed deep in the Earth). Uranium has a very long half-life of 4.5 billion years, which is more than long enough to date most rocks on Earth, though it is not reliable for dating rocks under 1 million years old.
Potassium-Argon (K-Ar) dating is also a useful method of dating rocks. Potassium-40 decays into two daughter isotopes, argon-40 and calcium-40. The daughter atom scientists use for radiometric dating is the argon-40 because (unlike calcium) it is rare within minerals. The reason for this is that argon is a noble gas and doesn’t normally bond with other elements; therefore, any argon-40 within a mineral is most likely from potassium-40 decay. The use of argon also has drawbacks. For instance a gas can easily escape from a rock. Therefore, special care needs to be taken in the lab to capture the argon-40 for analysis. The K-Ar radiometric dating system works well when dating rocks with potassium-rich mineral grains to analyze. For example, the igneous rock type granite is full of the potassium-rich pink mineral K-feldspar. A scientist dating K-feldspar in granite using K-Ar dating would date numerous mineral crystals in the rock to get their final estimated date for the rock. The half-life of potassium is 702 million years so the K-Ar system is most useful for dating older rocks (much like the U-Pb radiometric dating system).
All radiometric dating systems have error associated with them. Error is a term that describes the combination of factors relating to the sample chemistry, preservation, and analyses that can affect how accurate the results of the testing. It is best to think of radiometric dating results as scientific hypotheses that need to be tested further; a date should be supported by numerous additional date analyses to provide certainty in the accuracy. A major source of error for radiometric data analyses is addition or subtraction of either parent isotope atoms or daughter isotope atoms in the rock following its formation. This can occur in several ways; most commonly it happens when the rock is subjected to heat and pressure (metamorphism). There are ways to correct for these issues that allows the scientist to date both the rock and the metamorphic event as long as the geologic history is known. Analytical variability (error associated with quantifying the different isotopes in the rock) can also contribute some error to radiometric dating analyses. When scientists report radiometric dates they also provide a range of error (possible range of actual values) associated with their measurements (e.g., 4.10 ± 0.01 Ga, where Ga stands for gigaannum, or billions of years).
It is rare to find a rock that contains an amount of the parent remaining that falls exactly on one of the half-lives. In most cases we need to use a simple formula to calculate the age of a rock using the length of the half-life and the amount of parent remaining.
The formula is: ![]()
t1/2 = The length of the half-life in years
P = The proportion of the parent isotope remaining in decimal form. For example, if there is 50 % of the parent remaining it would equal 0.5.
Let’s work through a simple example using this equation that we already know the answer to in advance. You have a sample of bone that has 25% of the carbon-14 (half-life= 5730 years) remaining. How old is the sample? We can answer this question in two ways:
- We know that if there is 25% remaining, two half-lives have passed and with each half-life being 5730 the bone would be 11,460 years old.
- We could use the above equation and insert both the length of the half- life and the amount of the parent remaining:
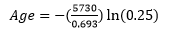
To solve the equation, take the natural Log (ln) of 0.25 and multiply by the term in the parentheses (make sure to include the negative sign). If you do this you will get 11,460 years as well.

