10.1 Standards of Quality and Statistics
Visit Audio Recordings for the audio version of this section.
LEARNING OBJECTIVES
- Define quality and grade.
- Define and explain how statistics are used in quality control.
- Estimate the likelihood of samples falling within one, two, or three standard deviations of the mean given a normal distribution caused by random factors.
Quality and Grade
According to the International Organization for Standardization (ISO), quality is “the degree to which a set of inherent characteristics fulfill requirements.”1 The requirements of a product or process can be categorized or given a grade to give a basis for comparison. The quality is determined by how well something meets the requirements of its grade.
Quality of Gasoline Grades

Petroleum refiners provide gasoline in several different grades based on the octane rating because higher octane ratings are suitable for higher compression engines. Gasoline must not be contaminated with dirt or water, and the actual performance of the fuel must be close to its octane rating. A shipment of low-grade gasoline graded as 87 octane that is free of water or other contaminants would be of high quality, while a shipment of high grade 93 octane gas that is contaminated with dirt would be of low quality.
For most people, the term quality also implies good value—getting your money’s worth. For example, even low-grade products should still work as expected, be safe to use, and last a reasonable amount of time. Consider the following examples.
Quality of Furniture Packing in John’s Move
John has antique furniture that is in excellent condition that was left to him by his grandmother. The pieces are important to John for sentimental reasons and they are also valuable. John decides to hire movers (high-grade professionals) to load his furniture into the truck using appropriate padding and restraints to prevent dents and scratches during the long trip to Saskatoon and then to unload the truck in Saskatoon. John’s standard for high quality is that no observable damage occurs to his large pieces of furniture, especially the antiques. If the furniture arrives in his new apartment without a single dent, scratch, or other damage, the activity will be of high quality. John’s standard for packing his kitchen is lower. His dishes are old and cheap, so he decides to trust his inexperienced friends (low-grade amateurs) to help him pack his kitchen. If a few of the dishes or glassware are chipped or broken in the process, the savings in labour cost will more than make up for the loss and were still a good value.
Statistics
Determining how well products meet grade requirements is done by taking measurements and then interpreting those measurements. Statistics—the mathematical interpretation of numerical data—is useful when interpreting large numbers of measurements and is used to determine how well the product meets a specification when the same product is made repeatedly. Measurements made on samples of the product must be between control limits—the upper and lower extremes of allowable variation—and it is up to management to design a process that will consistently produce products between those limits.
Instructional Designers often use statistics to determine the quality of their designs. Student assessments are one way in which instructional designers are able to tell whether learning occurs within the control limits.
Setting Control Limits in Gasoline Production
If a process is designed to produce a product of a certain size or other measured characteristic, it is impossible to control all the small factors that can cause the product to differ slightly from the desired measurement. Some of these factors will produce products that have measurements that are larger than desired and some will have the opposite effect. If several random factors are affecting the process, they tend to offset each other, and the most common results are near the middle of the range – this phenomenon is called the central limit theorem.
If the range of possible measurement values is divided equally into subdivisions called bins, the measurements can be sorted, and the number of measurements that fall into each bin can be counted. The result is a frequency distribution that shows how many measurements fall into each bin. If the effects that are causing the differences are random and tend to offset each other, the frequency distribution is called a normal distribution, which resembles the shape of a bell with edges that flare out. The edges of a theoretical normal distribution curve get very close to zero but do not reach zero.
Normal Distribution of Gasoline Samples
It is common to take samples — randomly selected subsets from the total population—and measure and compare their qualities, since measuring the entire population would be cumbersome, if not impossible. If the sample measurements are distributed equally above and below the center of the distribution as they are in Figure 10.1, the average of those measurements is also the center value that is called the mean, and is represented in formulas by the lowercase Greek letter µ (pronounced mu). The amount of difference of the measurements from the central value is called the “sample standard deviation” or just the “standard deviation”.
The first step in calculating the standard deviation is subtracting each measurement from the central value (mean) and then squaring that difference. (Recall from your mathematics courses that squaring a number is multiplying it by itself and that the result is always positive.) The next step is to sum these squared values and divide by the number of values minus one. The last step is to take the square root. The result can be thought of as an average difference. (If you had used the usual method of taking an average, the positive and negative numbers would have summed to zero.) Mathematicians represent the standard deviation with the lowercase Greek letter σ (pronounced sigma). If all the elements of a group are measured, instead of just a sample, it is called the standard deviation of the population and in the second step, the sum of the squared values is divided by the total number of values.
Figure 10.1 Normal Distribution of Measurements of Gasoline Samples
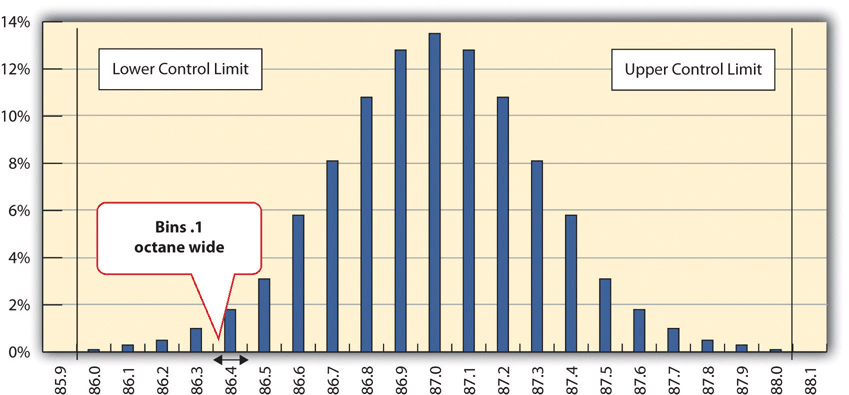
The chart shows that the most common measurements of octane rating are close to 87 and that the other measurements are distributed equally above and below 87. The shape of the distribution chart supports the central limit theorem’s assumption that the factors that are affecting the octane rating are random and tend to offset each other, which is indicated by the symmetric shape. This distribution is a classic example of a normal distribution. The quality control manager notices that none of the measurements are above 88 or below 86 so they are within control limits and concludes that the process is working satisfactorily.
Standard Deviation of Gasoline Samples
Figure 10.2 One Sigma Range
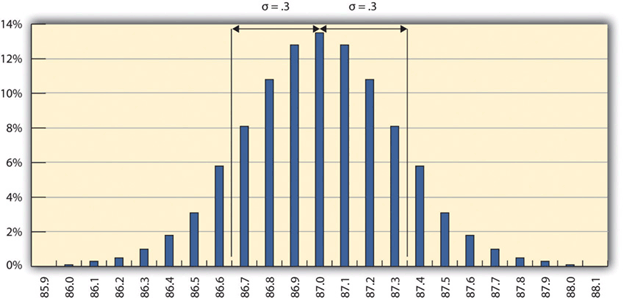
Most of the measurements are within 0.3 octane of 87.
For normal distributions, about 68.3% of the measurements fall within one standard deviation on either side of the mean. This is a useful rule of thumb for analyzing some types of data. If the variation between measurements is caused by random factors that result in a normal distribution and someone tells you the mean and the standard deviation, you know that a little over two-thirds of the measurements are within a standard deviation on either side of the mean. Because of the shape of the curve, the number of measurements within two standard deviations is 95.4%, and the number of measurements within three standard deviations is 99.7%. For example, if someone said the average (mean) height for adult men in the United States is 5 feet 10 inches (70 inches) and the standard deviation is about 3 inches, you would know that 68% of the men in the United States are between five feet seven inches (67 inches) and six feet one inch (73 inches) in height. You would also know that about 95% of the adult men in the United States were between five feet four inches and six feet four inches tall, and that almost all of them (99.7%) are between five feet one inches and six feet seven inches tall. These figures are referred to as the 68-95-99.7 rule.
Almost All Samples of Gasoline are Within Three STD
Figure 10.3 The 68-95-99.7 Rule
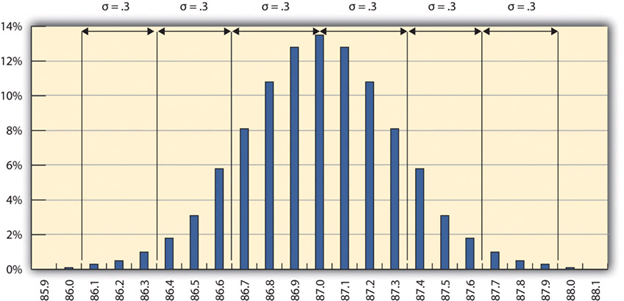
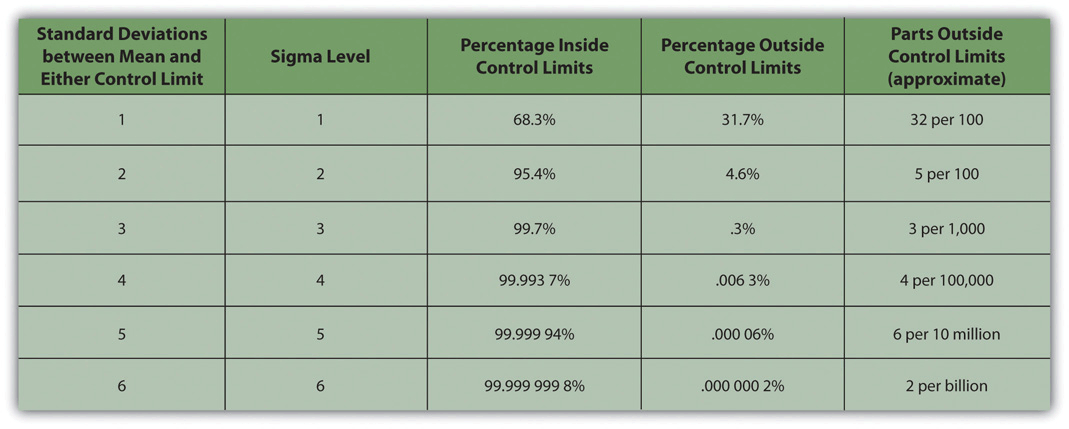
Some products must have less variability than others to meet their purpose. For example, if training designed to operate highly specialized and potentially dangerous machinery was assessed for quality, most participants would be expected to exceed the acceptable pass rate. Three standard deviations from the control limits might be fine for some products but not for others. In general, if the mean is six standard deviations from both control limits, the likelihood of a part exceeding the control limits from random variation is practically zero (2 in 1,000,000,000). (Refer to Figure 10.4)
Figure 10.4 Meaning of Sigma Levels
A Step Project Improves Quality of Gasoline
Figure 10.5 Smaller Standard Deviation
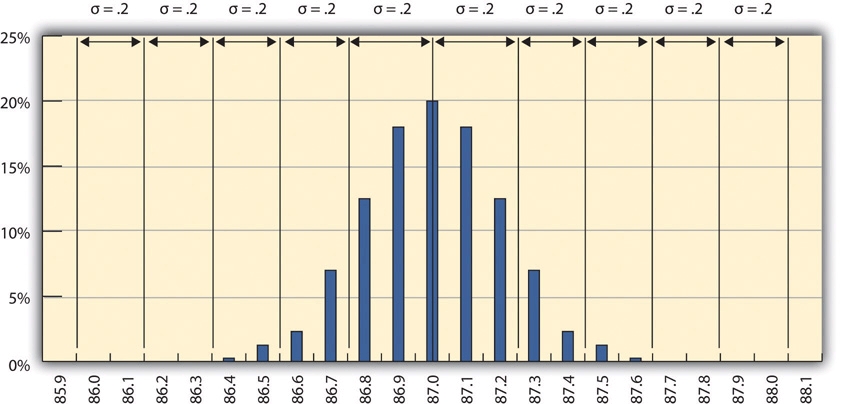
The refinery’s quality control manager calculates that the new standard deviation is 0.2 octane. From this, he can use the 68-95-99.7 rule to estimate that 68.3% of the fuel produced will be between 86.8 and 87.2 and that 99.7% will be between 86.4 and 87.6 octane. A shorthand way of describing this amount of control is to say that it is a five-sigma production system, which refers to the five standard deviations between the mean and the control limit on each side.
KEY TAKEAWAYS
- Quality is the degree to which a product or service fulfills requirements and provides value for its price.
- Statistics is the mathematical interpretation of numerical data, and several statistical terms are used in quality control. Control limits are the boundaries of acceptable variation.
- If random factors cause variation, they will tend to cancel each other out—the central limit theorem. The central point in the distribution is the mean, which is represented by the Greek letter mu, µ. If you choose intervals called bins and count the number of samples that fall into each interval, the result is a frequency distribution. If you chart the distribution and the factors that cause variation are random, the frequency distribution is a normal distribution, which looks bell shaped.
- The center of the normal distribution is called the mean, and the average variation is calculated in a special way that finds the average of the squares of the differences between samples and the mean and then takes the square root. This average difference is called the standard deviation, which is represented by the Greek letter sigma, σ.
- About 68% of the samples are within one standard deviation, 95.4% are within two, and 99.7% are within three.
[1] International Organization for Standardization, Quality Management Systems—Fundamentals and Vocabulary (Geneva: ISO Press, 2005), in Project Management Institute, Inc., A Guide to the Project Management Body of Knowledge (PMBOK Guide), 4th ed. (Newtown Square, PA: Project Management Institute, Inc., 2008), 190.
How well something meets the expected or specified requirements of its grade.
The mathematical interpretation of numerical data.
The management of production standards through statistical interpretation of random product measurements, which emphasizes consistency and accuracy.
Randomly selected subsets from the total population.
The calculated amount of difference of the measurements from the central value.
The upper and lower extremes of allowable variation.
If several random factors are affecting the process, they tend to offset each other, yielding the most common results near the middle of the range.
subdivisions of measured values.
How many measurements fall into each established category.
If a distribution of items is charted, and the factors that cause variation are random, the chart will resemble the shape of a bell.
For normal distributions, about 68.3% of the measurements fall within one standard deviation on either side of the mean; because of the shape of the curve, the number of measurements within two standard deviations is 95.4%, and the number of measurements within three standard deviations is 99.7%.

