1.5. Hybrid Orbitals

Covalent bonds involve the sharing of spin-paired electrons. This creates localized bonds, confined to the region between the bonded atoms, from an overlap of orbitals. The better the overlap between the orbitals, the stronger the bond (e.g. σ vs. π bonds discussed above).

This last part creates a problem for organic chemists. Most organic molecules are primarily made from hydrogen, carbon, oxygen, and nitrogen. The valence orbitals involved in bonding for these elements are s and p orbitals (Figure 1.22).

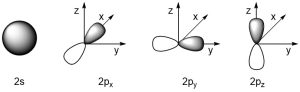
Figure 1.22 –Representations of 2s, 2p_x, 2p_y, and 2p_z Orbitals.

s Orbitals have a spherical shape and can be easily used to rationalize bonding from any direction. However, p orbitals exist as p_x, p_y, and p_z and are orthogonal (90°) from each other. Based on VSEPR theory, typical bond angles should be ~109° (tetrahedral geometries), ~120° (trigonal planar geometries), and 180° (linear geometries). We are thus left with a question of how to reconcile the strong σ bonds observed in these molecules with the apparent poor overlap of p orbitals at these geometries.

Orbital hybridization is one approach used to explain this discrepancy. Hybrid orbitals are a mathematical construct (a model) arising from the combination of 2s and 2p orbitals. Orbital hybridization is not a physical process. However, the model is much simpler to understand and discuss than the more rigorous (and accurate) approaches developed since.

The exact math behind how individual hybrid orbitals may be generated from atomic orbitals is interesting but not important for understanding. However, two important consequences of the approach should be noted.

First, the number of hybrid orbitals generated is exactly equal to the number of atomic orbitals used to make them. This means that in all cases we will start with four valence orbitals (2s, 2p_x, 2p_y, and 2p_z) and end with four valence orbitals (the new hybrid orbitals and any unused atomic orbitals). The new hybrid orbitals are used in forming σ bonds or contain lone pairs. Any p orbitals that remain are used in forming π bonds; p orbitals are not involved in σ bonds in hybridization models.

Second, in all cases the hybrid orbitals arise from the combination of an s orbital with one or more p orbitals. As a result, all of the hybrid orbitals look the same (Figure 1.23). In each case they resemble a ‘biased’ p orbital where one lobe is larger than before and the other is smaller than before. This is because one lobe combined constructively with the s orbital (both were the same phase) and one lobe combined deconstructively with the s orbital (the two were opposite phases). The only difference between hybrid orbitals is the directionality of the lobes.

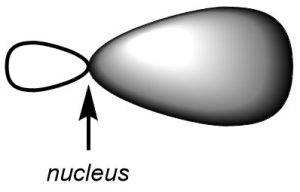
Figure 1.23 – Shape of a Hybrid Orbital.

1.5.1. sp³ Hybridization and Tetrahedral Geometries

If we combine the 2s orbital with the 2p_x, 2p_y, and 2p_z orbitals we get four sp³ orbitals (Figure 1.24). The four valence orbitals combine mathematically to form four equivalent hybrid orbitals, which are named sp³ orbitals because they are formed from mixing one s and three p orbitals.

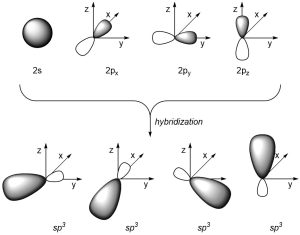
Figure 1.24 – sp³ Orbital Hybridization.

As a result of how the orbitals were combined, they each point in different directions. The angle between each orbital is now ~109°, which allows construction of tetrahedral geometries (Figure 1.25).

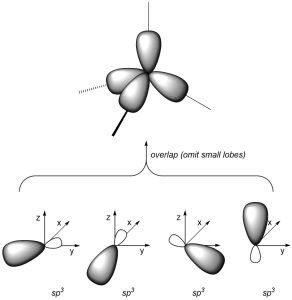
Figure 1.25 – Overlay of sp³ Orbital Geometry.

We can describe σ bonds made from the atom as arising from the overlap of one of its sp³ orbitals with an orbital from the adjacent atom. For example, the C-H σ bonds in methanol form from the overlap of a sp³ orbital on carbon with the s orbital on hydrogen (Figure 1.26). Conversely, the C-O σ bond forms from the overlap of an sp³ orbital from carbon with an sp³ orbital from oxygen (the oxygen has four groups around it, and so is also sp³ hybridized). Hybrid orbitals are not always involved in bonding and can instead localize lone pairs.

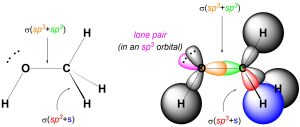
Figure 1.26 – σ Bond Formation and Lone Pair Placement Using sp³ Hybrid Orbitals.

1.5.2. sp² Hybridization and Trigonal Planar Geometries

If we combine the 2s orbital with the 2p_x and 2p_y orbitals (and leave the 2p_z orbital untouched) we get three sp² orbitals (Figure 1.27). The three valence orbitals combine mathematically to form three equivalent hybrid orbitals, which are named sp² orbitals because they are formed from mixing one s and two p orbitals. Note that the new hybrid orbitals exist only in the x/y plane.

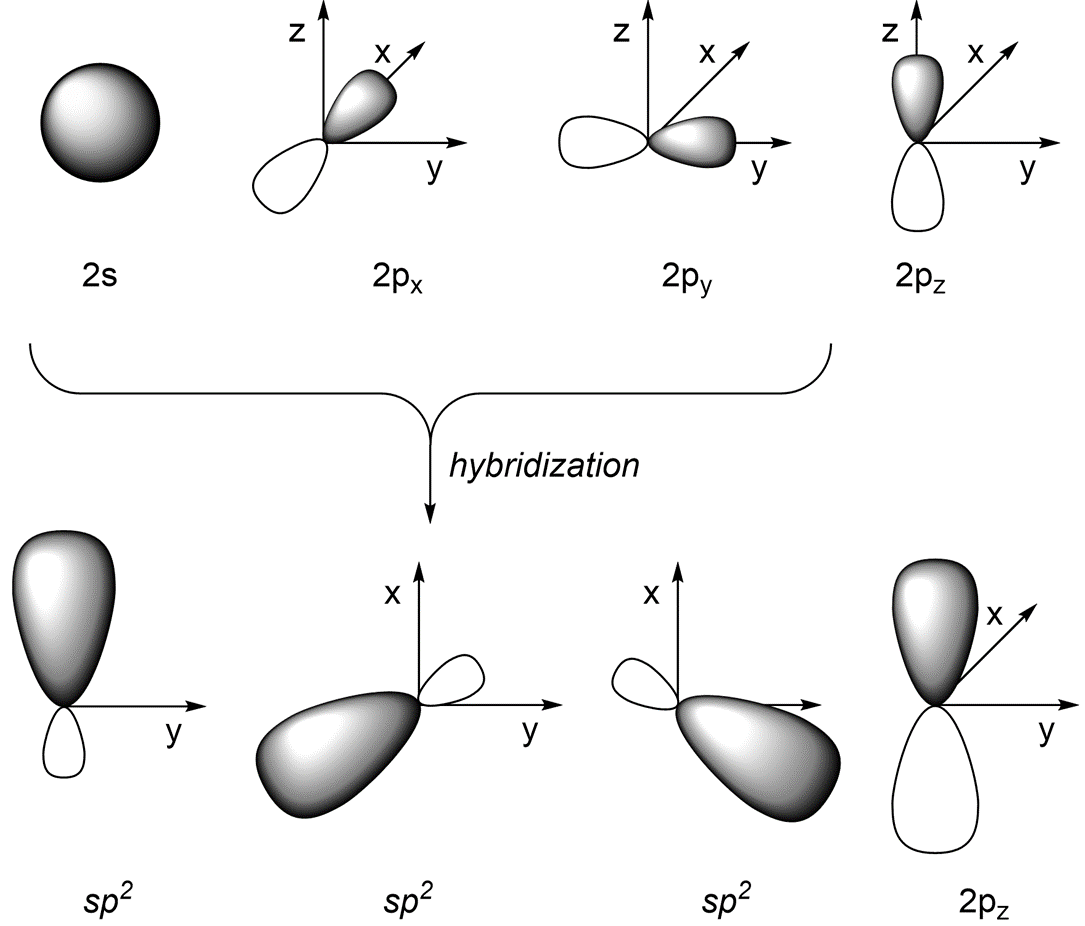
Figure 1.27 – sp² Orbital Hybridization.

As a result of how the orbitals were combined, they each point in different directions. The angle between each orbital is now ~120°, which allows construction of trigonal planar geometries (Figure 1.28). The remaining 2p_z orbital is perpendicular to the plane occupied by the sp² orbitals.

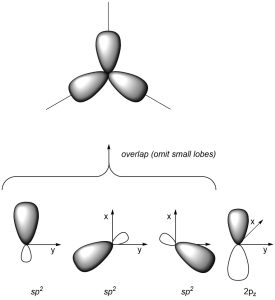
Figure 1.28 – Overlay of sp² Orbital Geometry.

We can describe σ bonds made from the atom as arising from the overlap of one of its sp² orbitals with an orbital from the adjacent atom. For example, the C-H σ bonds in formaldehyde form from the overlap of a sp² orbital on carbon with the s orbital on hydrogen (Figure 1.29). Conversely, the C-O σ bond forms from the overlap of a sp² orbital from carbon with a sp² orbital from oxygen (the oxygen has three groups around it, and so is also sp² hybridized). Hybrid orbitals are not always involved in bonding and can instead localize lone pairs. Finally, the C-O π bond forms from the overlap of the untouched 2p_z orbital on carbon with the corresponding 2p_z orbital on oxygen.

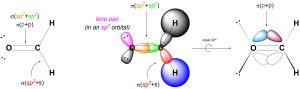
Figure 1.29 – σ and π Bond Formation and Lone Pair Placement Using sp² Hybrid Orbitals.

1.5.3. sp Hybridization and Linear Geometries

If we combine the 2s orbital with the 2p_x orbital (and leave the 2p_y and 2p_z orbitals untouched) we get two sp orbitals (Figure 1.30). The two valence orbitals combine mathematically to form two equivalent hybrid orbitals, which are named sp orbitals because they are formed from mixing one s and one p orbitals.

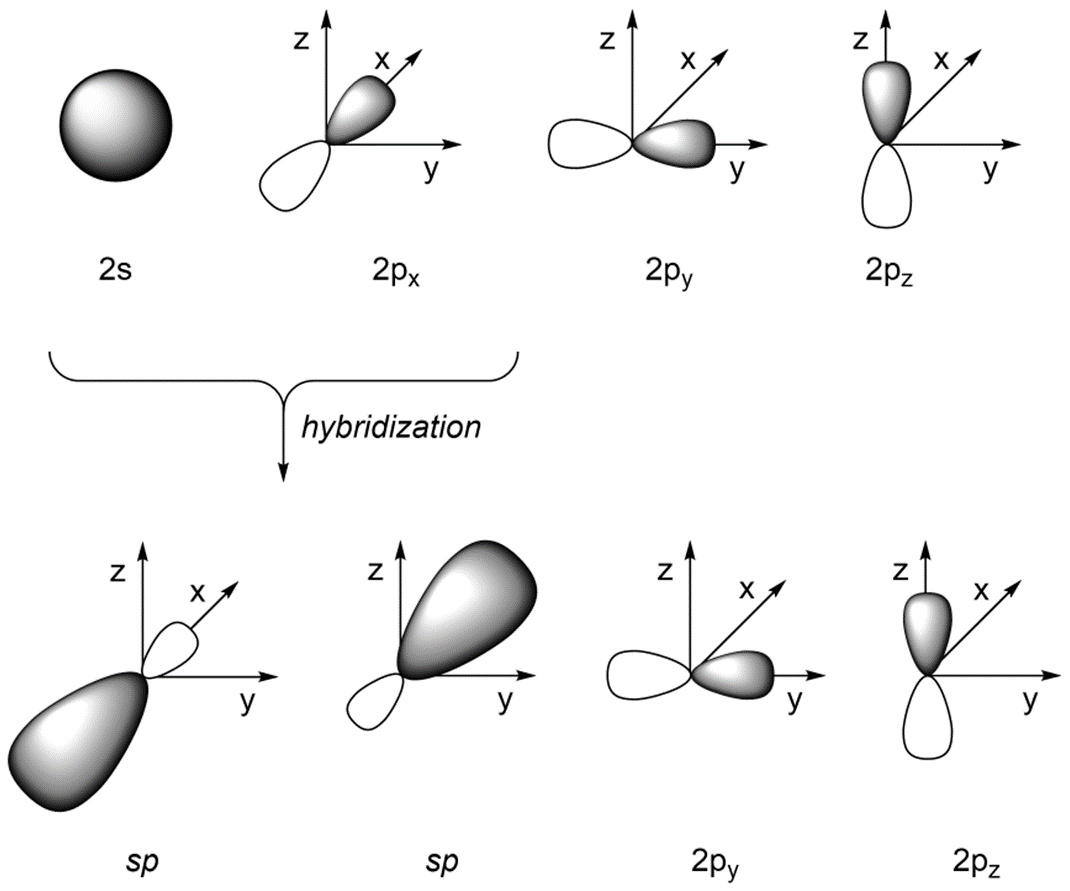
Figure 1.30 – sp Orbital Hybridization.

As a result of how the orbitals were combined, they point in different directions. The angle between the orbitals is now ~180°, which allows construction of linear geometries (Figure 1.31). The remaining 2p_y and 2p_z orbitals are perpendicular to the axis occupied by the sp orbitals and to each other.

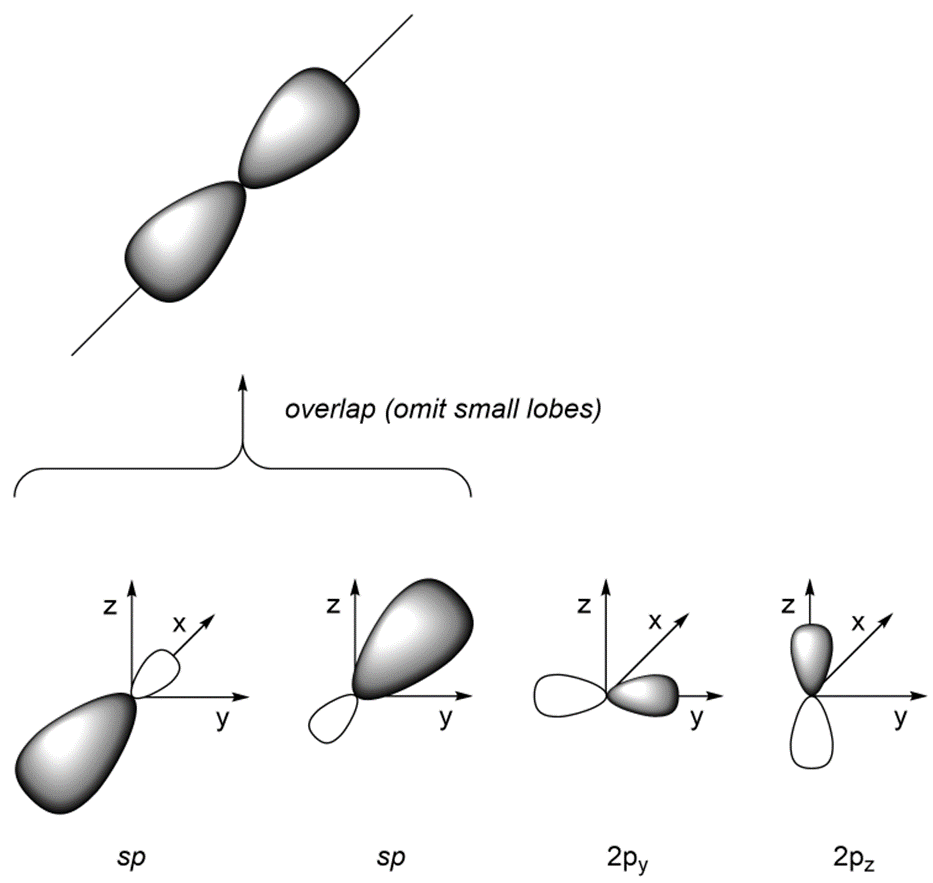
Figure 1.31 – Overlay of sp Orbital Geometry.

We can describe σ bonds made from the atom as arising from the overlap of one of its sp orbitals with an orbital from the adjacent atom. For example, the C-C σ bond in acetonitrile forms from the overlap of a sp orbital on the central carbon with the sp³ orbital on the other carbon (the other carbon has four groups around it, and so is sp³ hybridized; Figure 1.32). Conversely, the C-N σ bond forms from the overlap of a sp orbital from the central carbon with a sp orbital from the nitrogen (the nitrogen has two groups around it, and so is also sp hybridized). Hybrid orbitals are not always involved in bonding and can instead localize lone pairs. Finally, the C-N π bonds form from the overlap of the untouched p orbitals on carbon and nitrogen: the 2p_y orbitals on each combine to make one π bond, and the 2p_z orbitals on each combine to make the other π bond. Visualizing the three-dimensional orientation of localized bonds using two dimensional graphics can be challenging. It is important to remember that the two π bonds exist simultaneously in orthogonal planes (i.e. one is in a y plane and one is in a z plane).

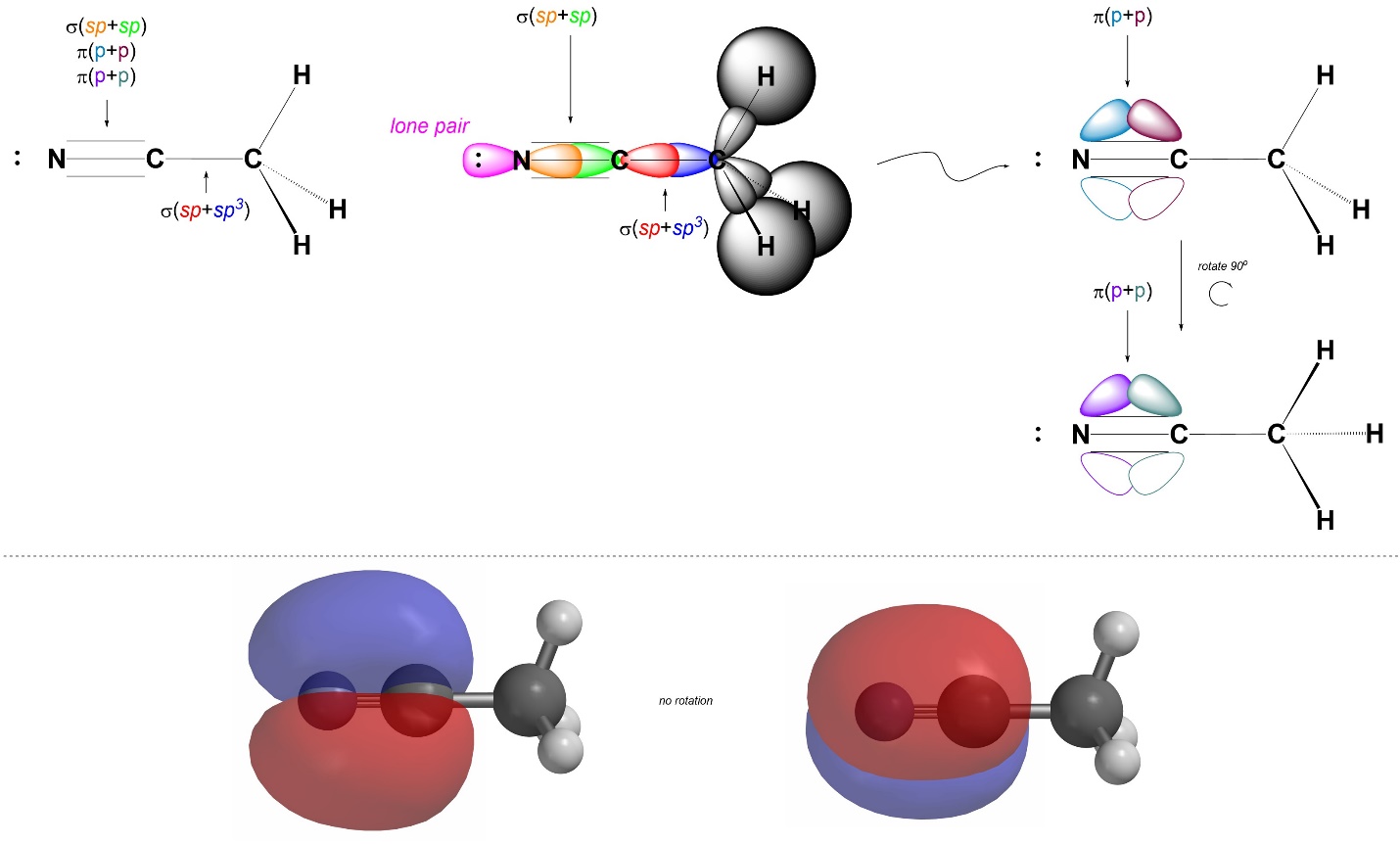
Figure 1.32 – σ and π Bond Formation and Lone Pair Placement Using sp Hybrid Orbitals.

1.5.4. How to Determine the Hybridization of an Atom in a Molecule

It is important to remember that orbital hybridization is a model used to rationalize the geometries we observe. For example, saying that a carbon atom is sp³ hybridized is a synonym for saying the geometry around that carbon is tetrahedral. There is thus a simple trick to quickly determine the hybridization state of any atom: count the number of connected groups. In this case ‘groups’ refers to any connected atom, regardless of how many bonds connect the two, and any lone pairs. The number of groups around it is equal to the sum of exponents in the hybridization name (Figure 1.33).

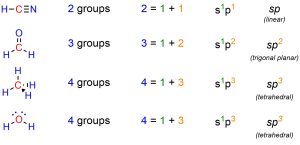
Figure 1.33 – Examples of Determining Hybridization State by Counting Attached Groups.